Pengertian hashing and hash table trees & binary tree

• Hashing

Ide utama dari hashing adalah mengubah suatu string menjadi suatu bilangan dengan suatu fungsi. Misalkan kita memiliki string "abca", dan fungsi f yang memetakan string ke bilangan bulat berikut:

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
f(S) = (                                                                                                    
  (banyaknya 'a')*1 +                                                                                  
  (banyaknya 'b')*2 + 
  (banyaknya 'c')*3 + 
  ... + 
  (banyaknya 'z')*26
) mod 1000000

Artinya:
f("abca") = (2*1 + 1*2 + 1*3 + 0*4 + 0*5 + ... + 0*26) mod 1000000
          = 7
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑


Kita berhasil mengubah string "abca" menjadi sebuah angka, yaitu 7. Hal ini juga akan dilakukan untuk setiap nama mahasiswa dalam setiap operasi; sebelumnya di-hash terlebih dahulu. Dengan demikian, direct addressing table dapat kembali digunakan! Kini kompleksitas untuk setiap operasi adalah O(K), dengan K adalah kompleksitas menghitung nilai hash melalui fungsi hashing. Untuk contoh di atas, K = panjang string. Jika panjang setiap string cukup kecil, setiap operasi bisa dianggap O(1).

1. Metode Hashing

Untuk mengatasi kerugian korespondensi satu-satu, digunakan hashing
Untuk mengurangi banyaknya ruang alamat yang digunakan untuk pemetaan dari key yang memiliki cakupan yang luas ke nilai alamat yang memiliki cakupan yang dipersempit
Untuk itu dibutuhkan fungsi HASH
Output fungsi HASH adalah home address dari record yang keynya diproses
Fungsi : f(key) = address

2. Macam-macam Fungsi HASH

• Fungsi modulo

Home address dicari dengan cara mencari sisa hasil bagi nilai key dengan suatu nilai tertentu.
Fungsi: f(key) = key mod n
Dengan n adalah:
Banyaknya ruang alamat yang tersedia
Atau bilangan prima terdekat yang berada di atas nilai banyak data, setelah itu banyaknya ruang alamat disesuaikan dengan n

• Fungsi Pengkuadratan

Home address dicari dengan mengkuadratkan setiap digit pembentuk key, lalu semua hasilnya dijumlahkan
Contoh: , semua digit dikuadratkan dan dijumlah
Fungsi Penambahan Kode ASCII
Jika key bukan kode numerik, home address dicari dengan menjumlahkan kode ASCII setiap huruf pembentuk key
ADE = = 192

⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺

• Hash Table

Hash table merupakan salah satu struktur data yang digunakan dalam penyimpanan data sementara. Tujuan dari hash table adalah untuk mempercepat pencarian kembali dari banyak data yang disimpan. Hash table menggunakan suatu teknik penyimpanan sehingga waktu yang dibutuhkan untuk penambahan data (insertions), penghapusan data (deletions), dan pencarian data (searching) relatif sama dibanding struktur data atau algoritma yang lain.

Kelebihan dari hash table antara lain sebagai berikut:

– Hash table relatif lebih cepat

– Kecepatan dalam insertions, deletions, maupun searching relatif sama

Hash table menggunakan memori penyimpanan utama berbentuk array dengan tambahan algoritma untuk mempercepat pemrosesan data. Pada intinya hash table merupakan penyimpanan data menggunakan key value yang didapat dari nilai data itu sendiri. Dengan key value tersebut didapat hash value. Jadi hash function merupakan suatu fungsi sederhana untuk mendapatkan hash value dari key value suatu data. Yang perlu diperhatikan untuk membuat hash function adalah:

– ukuran array/table size(m),

– key value/nilai yang didapat dari data(k),

– hash value/hash index/indeks yang dituju(h).

Berikut contoh penggunaan hash table dengan hash function sederhana yaitu memodulus key value dengan ukuran array : h = k (mod m)

Misal kita memiliki array dengan ukuran 13, maka hash function : h = k (mod 13).

Dengan hash function tersebut didapat :

k H

7 7

13 0

25 12

27 1

39 0

Perhatikan range dari h untuk sembarang nilai k.

Maka data 7 akan disimpan pada index 7, data 13 akan disimpan pada index 0, dst..

Untuk mencari kembali suatu data, maka kita hanya perlu menggunakan hash function yang sama sehingga mendapatkan hash index yang sama pula.

Misal : mencari data 25 → h = 25 (mod 13) = 12

Namun pada penerapannya, seperti contoh di atas terdapat tabrakan (collision) pada k = 13 dan k = 39. Collision berarti ada lebih dari satu data yang memiliki hash index yang sama, padahal seperti yang kita ketahui, satu alamat / satu index array hanya dapat menyimpan satu data saja.

Untuk meminimalkan collision gunakan hash function yang dapat mencapai seluruh indeks/alamat. Dalam contoh di atas gunakan m untuk me-modulo k. Perhatikan bila kita menggunakan angka m untuk me-modulo k maka pada indeks yang lebih besar dari dan sama dengan m di hash table tidak akan pernah terisi (memori yang terpakai semakin kecil), kemungkinan terjadi collision juga semakin besar.

Karena memori yang terbatas dan untuk masukan data yang belum diketahui tentu collision tidak dapat dihindari.

Berikut ini cara-cara yang digunakan untuk mengatasi collision :

1.   Closed hashing (Open Addressing)

Close hashing menyelesaikan collision dengan menggunakan memori yang masih ada tanpa menggunakan memori diluar array yang digunakan. Closed hashing mencari alamat lain apabila alamat yang akan dituju sudah terisi oleh data.

Kelemahan dari closed hashing adalah ukuran array yang disediakan harus lebih besar dari jumlah data. Selain itu dibutuhkan memori yang lebih besar untuk meminimalkan collision.

2.   Open hashing (Separate Chaining)

Pada dasarnya separate chaining membuat tabel yang digunakan untuk proses hashing menjadi sebuah array of pointer yang masing-masing pointernya diikuti oleh sebuah linked list, dengan chain (mata rantai) 1 terletak pada array of pointer, sedangkan chain 2 dan seterusnya berhubungan dengan chain 1 secara memanjang.

Kelemahan dari open hashing adalah bila data menumpuk pada satu/sedikit indeks sehingga terjadi linked list yang panjang.

⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺⟺

• Tree

Merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :

1. Prodecessor : node yang berada diatas node tertentu.

2. Successor : node yang berada di bawah node tertentu.

3. Ancestor : seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.

4. Descendant : seluruh node yang terletak sesudah node tertentu dan terletak pada jalur yang sama.

5. Parent : predecssor satu level di atas suatu node.

6. Child : successor satu level di bawah suatu node.

7. Sibling : node-node yang memiliki parent yang sama dengan suatu node.

8. Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua 

9. karakteristik dari tree tersebut.

10. Size : banyaknya node dalam suatu tree.

11. Height : banyaknya tingkatan/level dalam suatu tree.

12. Root : satu-satunya node khusus dalam tree yang tak punya predecssor.

13. Leaf : node-node dalam tree yang tak memiliki seccessor.

14. Degree : banyaknya child yang dimiliki suatu node.

• Binary Tree

Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut, maka tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.

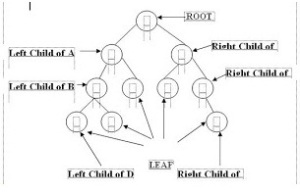
➨Operasi-operasi pada Binary Tree :

∘ Create : Membentuk binary tree baru yang masih kosong.

∘ Clear : Mengosongkan binary tree yang sudah ada.

∘ Empty : Function untuk memeriksa apakah binary tree masih kosong.

∘ Insert : Memasukkan sebuah node ke dalam tree. Ada tiga pilihan insert: sebagai root, left child, atau right child. Khusus insert sebagai root, tree harus dalam keadaan kosong.

∘ Find : Mencari root, parent, left child, atau right child dari suatu node. (Tree tak boleh kosong)

∘ Update : Mengubah isi dari node yang ditunjuk oleh pointer current. (Tree tidak boleh kosong)

∘ Retrieve : Mengetahui isi dari node yang ditunjuk pointer current. (Tree tidak boleh kosong)

∘ DeleteSub : Menghapus sebuah subtree (node beserta seluruh descendantnya) yang ditunjuk current. Tree tak boleh kosong. Setelah itu pointer current akan berpindah ke parent dari node yang dihapus.

∘ Characteristic : Mengetahui karakteristik dari suatu tree, yakni : size, height, serta average lengthnya. Tree tidak boleh kosong. (Average Length = [jumlahNodeLvl1*1+jmlNodeLvl2*2+…+jmlNodeLvln*n]/Size)

∘ Traverse : Mengunjungi seluruh node-node pada tree, masing-masing sekali. Hasilnya adalah urutan informasi secara linier yang tersimpan dalam tree. Ada tiga cara traverse : Pre Order, In Order, dan Post Order.

Sumber:
https://saragusti22.wordpress.com/2015/05/04/pengantar-struktur-data-tree-dan-binary-tree/
https://sourcecodegeneration.blogspot.com/2018/08/pengertian-binary-tree-binary-search.html